The deMon2k Home Page Home | Program | Download | Support | Online Manual | Tutorials | News & Events | Publications |Mailing List| Developers

Program :: Program description | Features of deMon2k | deMon2k citations | Program branches | History

Program description

deMon (density of Montréal) is a software package for density functional theory (DFT) [1-3] calculations. It uses the linear combination of Gaussian-type orbital (LCGTO) approach for the self-consistent solution of the Kohn-Sham (KS) DFT equations. The calculation of the four-center electron repulsion integrals is avoided by introducing an auxiliary function basis for the variational fitting of the Coulomb potential [4-6].

Program features

Some of the particular features of deMon2k are:

• Quantum Mechanical (QM), Molecular Mechanical (MM) and hybrid QM/MM energy models in one software package
• Variational density fitting for Coulomb and Fock potential avoids the calculation of four-center electron repulsion integrals (ERIS)
• LCGTO Kohn-Sham and Auxiliary Density Functional Theory (ADFT) as well as Harthree-Fock theory available
• Large selection of LDA, GGA, mGGA and hybrid functionals for Kohn-Sham and ADFT; Empirical dispersion corrections for all elements
• Restricted, unrestricted, restricted open-shell and constrained unrestricted self-consistent field (SCF) method for all ab-initio approaches
• Automatic generation of auxiliary function sets for Coulomb and Fock potential fitting
• Analytical three-center ERI recurrence relations without l limitation and double asymptotic expansion
• Half-Numerical ECP and MCP integral recurrence relations without l limitation
• Adaptive (and fixed) atom centered grids for the numerical integration of exchange-correlation functionals
• Local structure optimization and transition state search with (quasi) Newton restricted step algorithm
• Double ended saddle interpolation for the authomatic search of non-intuitive transition states
• Intrinsic reaction coordinate calculations
• Born-Oppenheimer molecular dynamics (BOMD) and QM/MM molecular dynamics (NVE,NVT); BOMD property calculations
• Time-dependent ADFT (TD-ADFT) for the calculation of UV/VIS spectra
• Auxiliary Density Perturbation Theory (ADPT) for the calculation of static and dynamic polarizabilities (α,β) and Fukui functions
• Non-Iterative Approach to Coupled-Perturbed Kohn-Sham (NIA-CPKS) for static dipole-dipole and dipole-quadrupole polarizabilities
• Nuclear magnetic resonance (NMR), magnetic shielding and molecular magnetizability from ADFT-GIAO
• Rotational g tensor and nuclear spin-rotation constants from ADFT-GIAO
• X-ray absorption and emission spectrum calculation
• Thermodynamic functions from the polyatomic ideal gas approximation and BOMD simulations
• Electric moments, DOS and population analyses (Mulliken, Löwdin, NBO, Bader, Voroni, Becke, Hirshfeld, etc.)
• Visualization of molecular fields and topological analysis of the electron density and electrostatic potential
• Interface to visualization software (Molden, Molekel, Vu, XAIM) and CHARMM
• Fully MPI pararellized code portable to various computer platforms and operating systems
• DFT optimized basis sets and utility software

Other features:

Additionally, several other features are implemented in private versions of deMon2k. Some of these features are:

• Constrained ADFT
• Dispersion interactions
• Electron propagator
• Fractional charge calculation
• Hybrid QM/MM with polarizable force field with the charge point dipole model of induction
• Metadynamics combined with ADFT and Density Functional Tight-Binding Methods
• Multicomponent ADFT
• Range-separated functionals
• Real-Time TD-ADFT for attosecond electron dynamics simulations
• Revised local hardness and hardness kernel definitions
• Several variants of the α function introduced by J.P. Perdew in mGGA
• Static and dynamic first hyperpolarizabilities from TD-ADPT

Required deMon2k citations

Any publication reporting results obtained with the deMon2k program must include, on depending of the used version of the software, one of the citations listed below.

Any reference to the deMon2k code should include the appropriate release version information.

In addition, all specific program functionalities, exchange-correlation functionals, basis sets and auxiliary function sets must also be cited appropriately, in case they have been used.

Version 6.x (Development Version):

Version 5.x (Public Release):

Version 4.x:

Version 3.x:

Version 2.x:

Program branches and related programs

The deMon2k program is developed by scientific groups all over the world. The current master version of deMon2k is described and can be downloaded from this web site. However, there exist several deMon2k branches and programs related to deMon2k, which have a different or extended functionality and might be based on an older master version. Please, see the following links for details and more information about functionality and reference to a deMon2k version number:

Program branches

• StoBe
• deMon@Grenoble
• deMonNano

Related programs

• Molden (Visualization program, interface in deMon2k available)
• Molekel (Visualization program, interface in deMon2k available)
• Vu (Visualization program, interface in deMon2k available)
• PUPIL (Program for linking together QM & MM programs)
• MSINDO (Semiempirical SCF MO program)

History

The game of the name

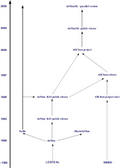
The first widely available version of deMon [7] appeared in 1992. deMon stands for densité de Montréal. The unusual capitalization emphasizes the roots of the code at the Université de Montréal (UdM) simultaneously by its implicit separation into two words [de-Mon(réal)] and by its resemblance to the main edifice of UdM with its tall central tower.

Program history

One way to understand deMon is to look at it in its historical context [8]. During the 1970's Slater's X method had been tried and abandoned by quantum chemists. Part of the difficulty was in the scattered wave, muffin-tin implementation of the time. Major numerical improvements came about through the introduction of Gaussian-type orbitals (GTO) and the use of auxiliary fitting functions in the LCAO-X program [9,10]. This allowed GTO technology to be borrowed from existant ab initio codes. Other major advances were Axel Becke's introduction of efficient, accurate, atom-centered numerical integration, Vosko, Wilk and Nusair's parameterization of the local density approximation [11] based upon Ceperly and Alder's accurate quantum Monte Carlo calculations of the correlation energy of the homogeneous electron gas, as well as the emergence of good quality generalized gradient approximations such as those of Becke [12] and Perdew [13]. By the 1980's, it had become clear that it was time to update the old LCAO-X strategy and write a modern DFT program with analytic derivatives capable of automatic geometry optimizations. This goal was realized simultaneously in deMon and in another program (namely DGauss developed at Cray for use on their computers).

Shortly after its appearance the original deMon code was substantially modified for commercialization by BIOSYM Technologies. The beta-release of this version appeared in 1993. It was the basis of the deMon-KS1 [14] series of programs developed in Montreal until 1997. Meanwhile the original deMon version was further developed in Montpellier and Stockholm. These developments were initially independent from each other. In 1997 they merged to become the deMon-KS3 [15] series of programs.

Over the years, many important method developments in DFT can be attributed to work originating with deMon and related programs. This includes, but is not limited to, NMR chemical shifts [16] and time-dependent density functional theory [17]. Several different versions of deMon developed.

The AllChem [18] project started in Hannover in 1995 independently of the deMon project. The aim of this project was to write a well structured DFT code from scratch. The first AllChem version appeared in 1997. The structured programming of AllChem proved very useful for the development and testing of new DFT approaches and algorithms.

The deMon and AllChem developers agreed at the first deMon Developers meeting in Ottawa to merge their codes in order to keep a Tower of Babel from arising. As a result the new code couples the deMon functionality with the stable and efficient integral part from AllChem, including for example f, g and higher angular momentum type hermite Gaussian auxiliary functions. The merged code was presented for the first time at the third deMon Developers meeting in Geneva. The present version of the code is now known as deMon2k [19] to distinguish it from the earlier (premerge) codes.

References